本文内容:
什么是向量
两个视角:有向线段;数据点
基本运行:向量加法、数量乘法
基本性质
零向量
我们将从向量开始进入线性代数的学习,学习过程中会使用Python语言进行部分代码实现,本文也会介绍部分Python语言相关的语法。
什么是向量?
基本定义
线性代数这所以重要,是因为它将数的研究从一个数拓展到了一组数。这里给出一个相对不是很严谨的定义:
向量(Vector)就是一组数的基本表示方法。
更严谨的定义:
“向量是线性代数中研究的基本对象,在具体计算中通常表示为一组有序的数(如坐标),但它本质上是满足向量空间公理的数学对象。”
研究一组数空间有什么用?最基本的出发点就是表示方向。
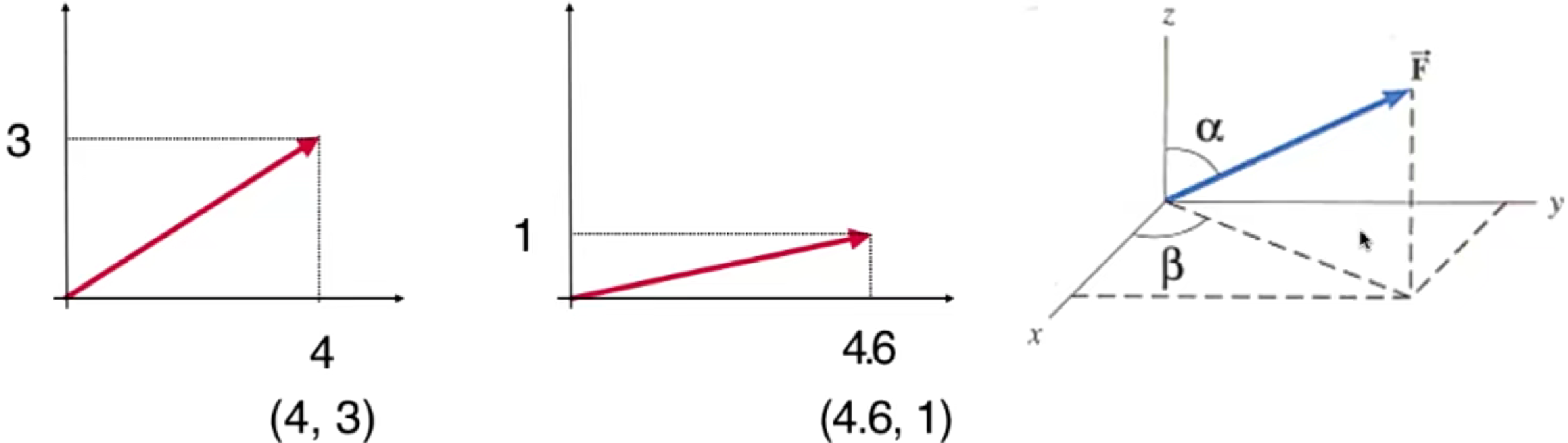
可以看到,虽然长度是一样的,但是方向不同,落在坐标系中的点是不同的。像物理中所学习的位移、速度、加速度、力这些都是既有大小又有方向的量。
起始点
向量的起始点重要么?在向量的研究中是不重要的。
从(-1,-1)到(3,2)和从(0,0)到(4,3)是一样的,只是坐标系不同。向量只是表征一个点到另外一个点的结果,而不区分这个过程是从哪一个起始点出发的。为了研究方便,我们约定向量都是从原点起始。但是顺序是重要的!(4,3)和(3,4)是截然不同的,向量是一组有序的数。
表示方向时,三个维度足以描述我们日常物理空间中的方向。然而,在数学和许多科学领域中,将概念推广到n维向量具有重要的理论和实际意义。高维向量可以表示多变量数据、复杂系统的状态或抽象的数学对象。虽然无法在三维以上的空间中直接可视化这些向量,但通过数学定义和运算,我们能够有效地处理和分析它们。高维向量的引入扩展了我们的表达能力,使得能够描述和解决更加复杂和多维度的问题。
我们可以举例说明:

一个房子可能有多个属性,根据上表我们可以表示成 (120,3,2,2,666),也就是说我们使用5个维度的向量来刻画一个个的房子。此时,向量就是一组数,这组数的含义同使用者定义。
看待向量的两个视角
几何视角(有大小和方向的量)
代数视角(有的数字/坐标)
无论如何,向量都是一组有序的数字。一个角度是它是一个有大小的方向,另一个角度是它仅仅是一组有序的数字,可以理解成在一个高维空间中的坐标点。两角度看似不同,但可以相互转换。一个方向就是一个点,而空间中的一个点,就可以看做从原点指向这个点的一个方向。
在实际的使用线性代数时,更多的是使用视角二(把每个向量看作空间中的一个点)。但是在学习向量的基本性质的时候,我们使用方向的视角会更直观、更形象,我们可以直接在二维或者三维的空间中绘制出对应的向量,直观的看到效果再推广到n维向量。
更关键的是:这两个视角,都不是简单的“一组数”。
一个是一个有向线段
一个是空间中的点
向量的更多术语和表示法
更严格的一些定义
和向量对应,一个数字,称为标量
代数,用符号代表数。和标量相区别,向量的符号画箭头:\vec{v}
个别情况下,尤其是几何学中,我们会考虑向量的起始点
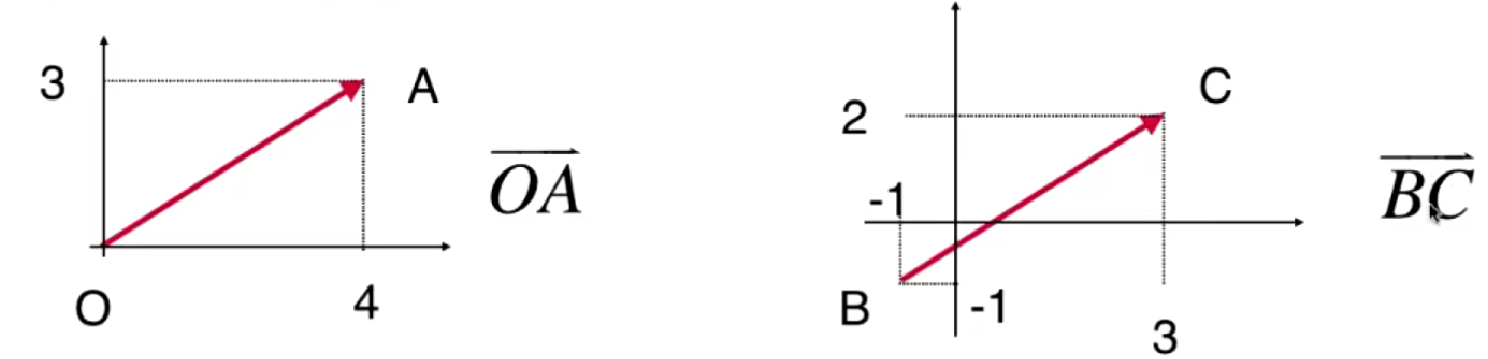
解析几何中,\vec{OA}和\vec{BC}是两个不同的向量,但是线性代数中可以不考虑原点
行向量和列向量
(x_1, x_2, \dots, x_n)
\begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix}
在现阶段的学习,没有区别,到了后面的矩阵学习才会有区别。
通常教材,论文,提到向量,都指列向量。由于横版印刷原因,通常使用转置符号表示:(3,4)T
实现属于我们自己的向量类
代码结构说明,首先创建一个playLA包,我们在此包内定义Vector向量类,在包外面创建测试脚本。
Vector类代码如下:
class Vector:
# list是python内置函数,这里使用lst命名
def __init__(self, lst):
self._values = lst
def __getitem__(self, index):
"""取向量的第index个元素"""
return self._values[index]
def __len__(self):
"""返回向量长度(有多少个元素)"""
return len(self._values)
# 系统调用
def __repr__(self):
return "Vector({})".format(self._values)
# 用户调用
def __str__(self):
return "({})".format(", ".join(str(e) for e in self._values))
测试脚本,main_vector.py 代码如下:
from playLA.Vector import Vector
if __name__ == "__main__":
vec = Vector([5, 2])
print(vec)
print("len(vec) = {}".format(len(vec)))
print("vec[0] = {}, vec[1] = {}".format(vec[0], vec[1]))
"""
(5, 2)
len(vec) = 2
vec[0] = 5, vec[1] = 2
<class 'playLA.Vector.Vector'>
(5, 2)
"""
这里我们简单回顾一下python的一些语法细节:
pyhon中本身是没有私有属性的,单下划线开头命名的变量名是类中私有的(不继承)
list是python内置函数,变量命名应该避免使用弱关键字
__repr__与__str__的区别:可以直接在终端中看效果
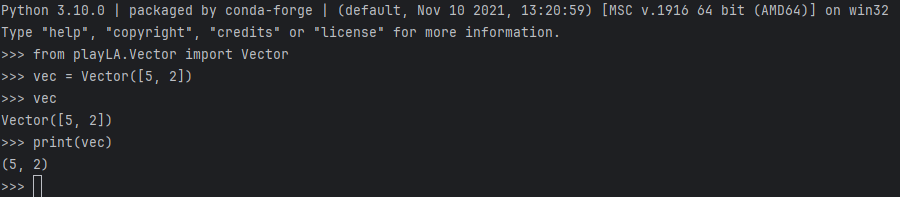
向量的两个基本运算
向量加法
思考一个问题:(5,2)T + (2,5)T = ?
在高中物理的时候,学习过两个向量相加,是以这两个向量为边的平行四边形的对角线上相应的向量。
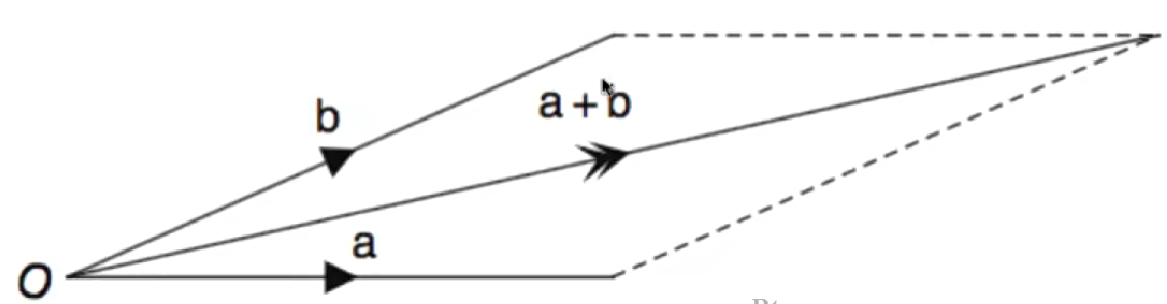
下面我们在二维坐标中理解这个结论:
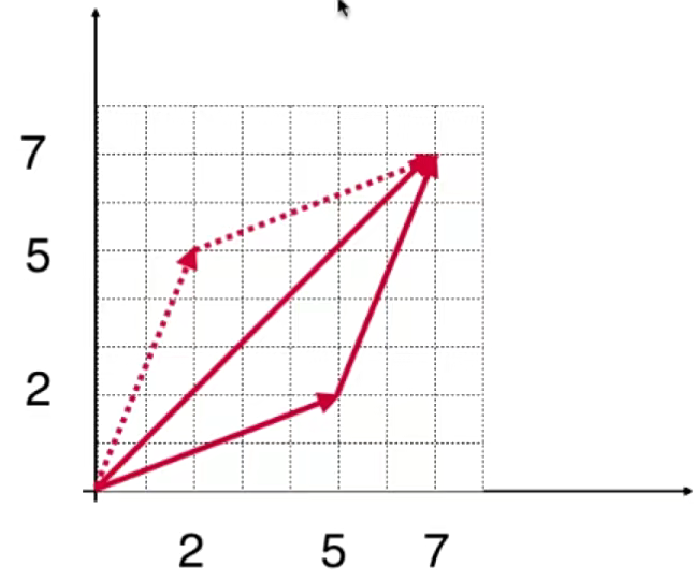
(5,2)T + (2,5)T 其实就相当于从原点出发,先往X轴方向走5个单位长度,再往Y轴方向走2个单位长度,到达(5,2)这个点;接着再从(5,2)这个点出发,沿X轴走2个单位长度,再沿Y轴走5个单位长度,最终就到了(7,7)这个点,所以相当于总共向X轴移动了7个单位,向Y轴也移动了7个单位。即:(5,2)T + (2,5)T = (7,7)T ,同理将结果推广到n维向量,就可以得到向量加法的定义:
\begin{pmatrix} v_1 \\ v_2 \\ \dots \\ v_n \end{pmatrix} + \begin{pmatrix} u_1 \\ u_2 \\ \dots \\ u_n \end{pmatrix} = \begin{pmatrix} v_1+u1 \\ v_2+u2 \\ \dots \\ v_n + u_n \end{pmatrix}
数量乘法
思考一个问题:2 × (5,2)T = ?
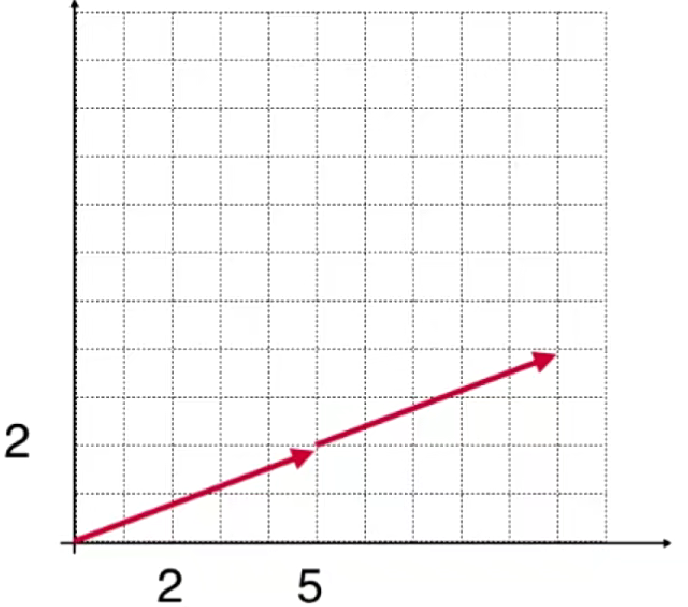
过程分析:
向x移动2次5个单位
再向y移动2次2个单位
总共向x移动10个单位
总共向y移动4个单位
基于以上过程可以得出:k × (a,b)T = (ka,kb)T
n维向量同理:
k \cdot \begin{pmatrix} v_1 \\ v_2 \\ \dots \\ v_n \end{pmatrix} = \begin{pmatrix} k \cdot v_1 \\ k \cdot v_2 \\ \dots \\ k \cdot v_n \end{pmatrix}
注意:
向量的加法两个操作数都是向量
而数量乘法一个操作是标量,一个操作数是向量
实现向量的基本运算
我们将会设计一个不可变(immutable)的向量类,所以操作的方法都会返回一个新的向量。下面分别实现相量的加法、减法与数量乘法。
向量加法实现
向量Vector类中增加下面的代码:
# list是python内置函数,这里使用lst命名
def __init__(self, lst):
self._values = list(lst)
# 重写些方法,可以重载+运算符
def __add__(self, another):
"""向量加法,返回结果向量"""
assert len(self) == len(another), \
"Error in adding. Length of vectors must be same."
# return Vector([a + b for a, b in zip(self._values, another._values)])
# Vector是可迭代的(不声明迭代器这里也可以正常工作,这是因为有__getitem__方法,但是符合规范还是要重写重写__iter__)
return Vector([a + b for a, b in zip(self, another)])
def __iter__(self):
"""返回向量的迭代器"""
return self._values.__iter__()
为了满足不可变的要求我们改造了构建方法,创建了一个新的lst。
另外我们重新了__iter__方法,让向量是可迭代的。
zip方法是将两个可迭代对象合成数据对。
向测试脚本main_vector.py 中增加:
vec2 = Vector([3, 1])
print("{} + {} = {}".format(vec, vec2, vec + vec2))向量减法实现
根据初等数学,我们可以很容易的定义出向量的减法运算,减法就是加法的逆运算。
def __sub__(self, another):
"""向量减法,返回结果向量"""
assert len(self) == len(another), \
"Error in subtracting. Length of vectors must be same."
return Vector([a - b for a, b in zip(self, another)])向测试脚本main_vector.py 中增加:
print("{} - {} = {}".format(vec, vec2, vec - vec2))数量乘法实现
数量乘法要注意的是,乘法是满足交换律的,所以要重写__mul__和__rmul__这两个方法。另外可以额外实现对向量取正和取负的操作方法。
def __mul__(self, k):
"""返回数量乘法的结果向量:self * k"""
return Vector([k * e for e in self])
def __rmul__(self, k):
"""返回数量乘法的结果向量:k * self"""
return self * k
def __pos__(self):
"""返回向量取正的结果向量"""
return 1 * self
def __neg__(self):
"""返回向量取负的结果向量"""
return -1 * self测试:
print("{} * {} = {}".format(vec, 3, vec * 3))
print("{} * {} = {}".format(3, vec, 3 * vec))
print("+{} = {}".format(vec, +vec))
print("-{} = {}".format(vec, -vec))向量运算的基本性质
从向量的两个基本运算出发,能够推导出一些基本性质,下面我们直接给出结论:
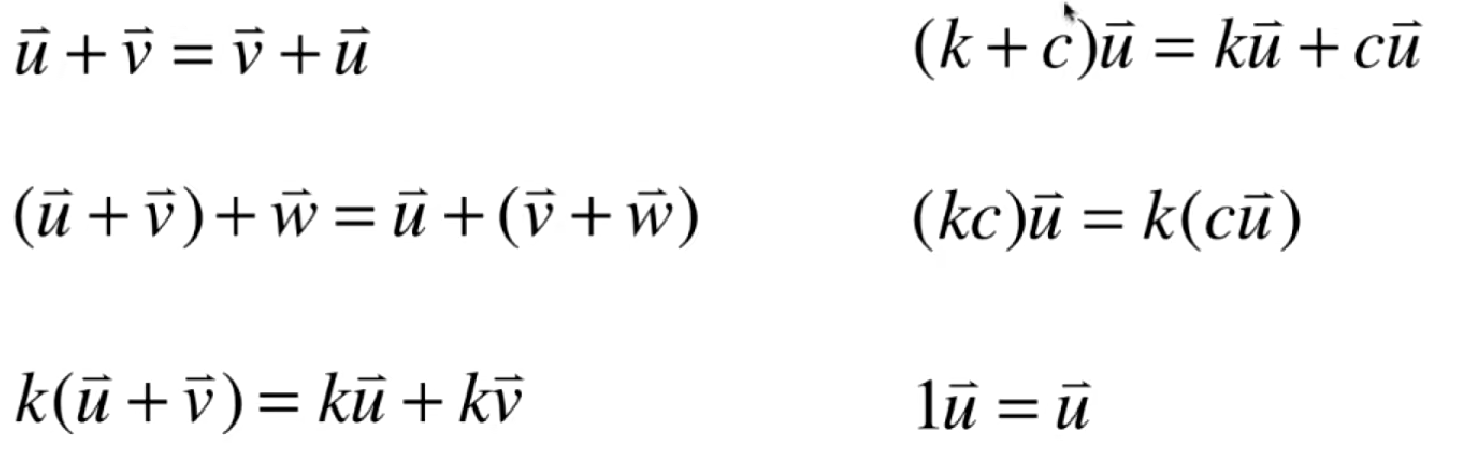
虽然很多结论是显而易见的,但是数学是一门严谨的学科,这些结论都可以进行证明的。
零向量
我们不定义什么是零向量,而是从推导一个性质出发:
对于任意一个向量\vec{u},都存在一个向量{O},满足:\vec{u} + O = \vec{u}。通过证明可以知道{O}应该是如下定义:
{O} = \begin{pmatrix} 0 \\ 0 \\ \dots \\ 0 \end{pmatrix}
我们称这个向量,为零向量。要注意的是这个零向量{O}是没有箭头的,到底有多少个0也是根据研究的空间维度有关的。
进而可以得出另外一个性质:
对于任意一个向量\vec{u},都存在一个向量-\vec{u},满足:\vec{u} + -\vec{u} = O。
上述的-\vec{u}也是唯一的。
实现零向量
零向量应该是针对类来说的,任意维度的向量都可以有对应的零向量,也就是说这个方法应该是属于类的。
向量Vector类中添加zero方法:
@classmethod
def zero(cls, dim):
"""返回一个dim维的零向量"""
return cls([0] * dim)测试代码:
zero2 = Vector.zero(2)
print(zero2)
print("{} + {} = {}".format(vec, zero2, vec + zero2))练习
复习Python面向对象相关的语法
自己动手实现Vector类
使用JavaSrcipt、TypeScript、Java实现自己的向量类